Minimalkosten-Fluss-Problem

Minimiere über den Fluss, sodass die Kosten $w_a$ minimal werden ${\min }_x{\sum }_{a\in A}{w}_a{x}_a$

Nebenbedingungen s.t. Die Bedarfsfunktion muss erfüllt werden. $x\left({\delta }^{\text{out }}(v)\right)-x\left({\delta }^{\text{in }}(v)\right)=b(v)$ für alle $v\in V$, Die Kapazitätsbedingung muss natürlich auch gelten $0\le x_a\le c_a$ für alle $a\in A$

Reformulierungen

auf (s-t)-Problem

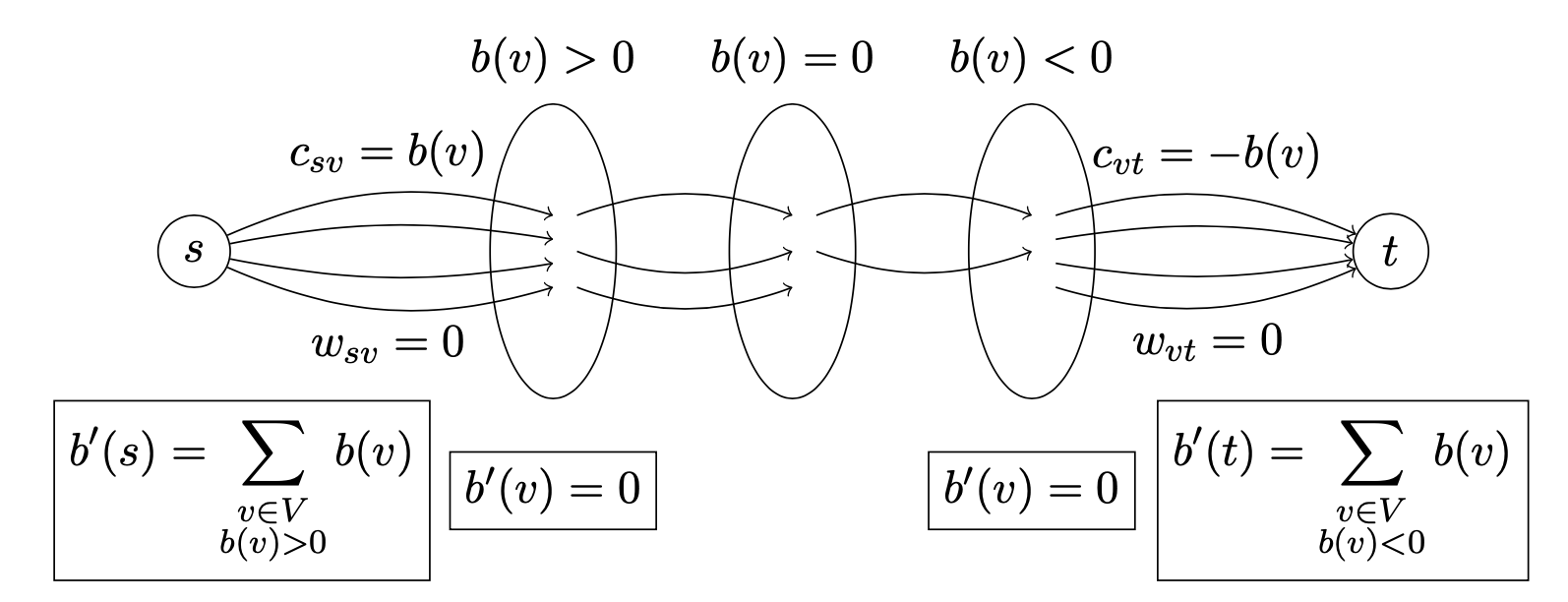
Zum eingrenzen der Bedarfsfunktion können Superquellen und Supersenken verwendet werden. Diese verbinden alle Quellen und Senken jeweils zu einem Knoten. Die Bedarfsfunktionen werden jeweils so gewählt, dass der Bedarf an den Quellen und Senken Null ist. Die Superquelle speist also alle Quellen und die Supersenke nimmt alles aus den Senken entgegen. Die Knoten zwischen den Quellen und Senken haben dank der Flusserhaltungsbedingung automatisch einen Bedarf von Null.

Der Bedarf der Superquellen und Supersenken wird natürlich durch die Summe der Bedarfe der Quellen und Senken definiert.

Minimalkosten-Zirkulations-Problem