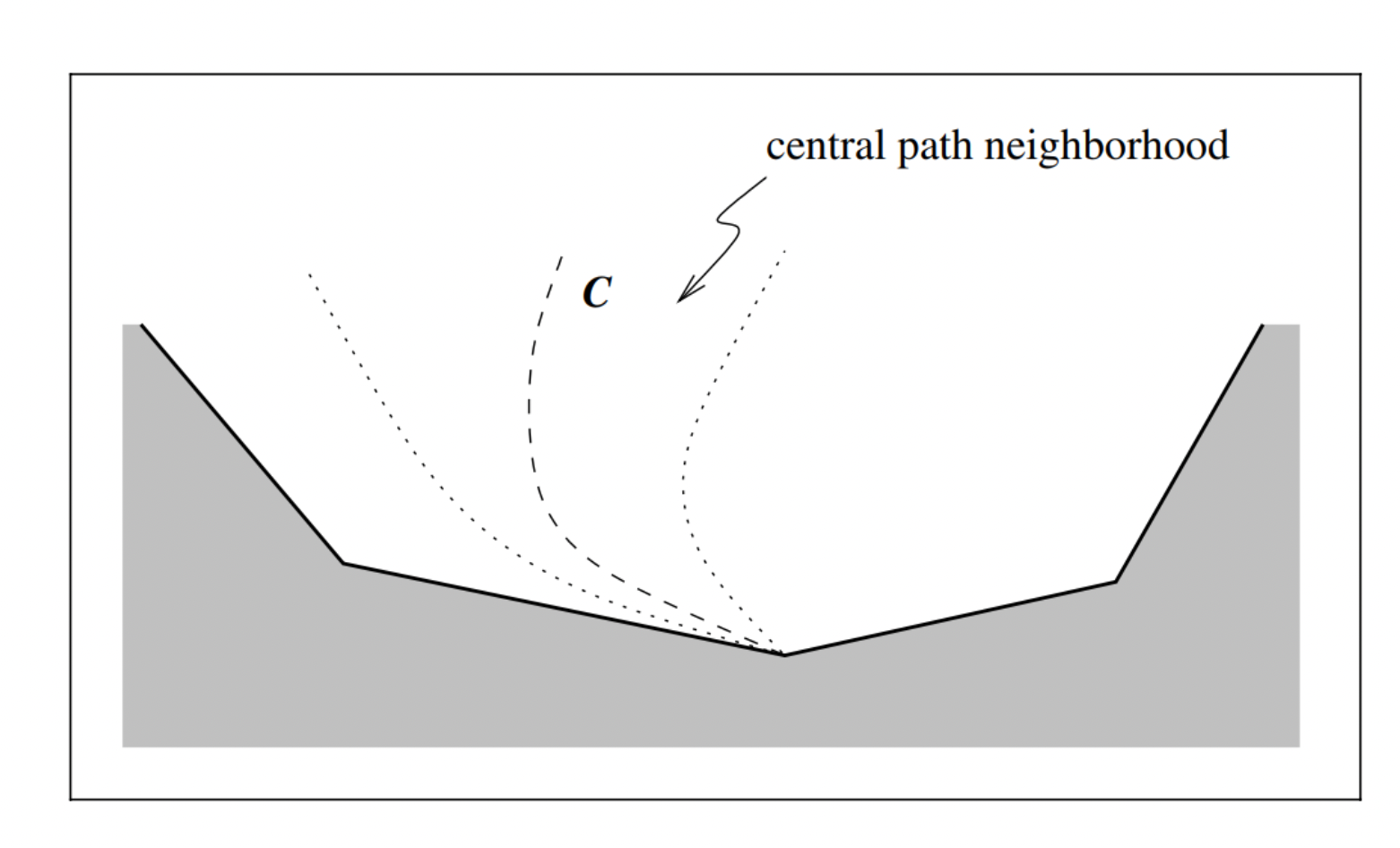
Zentraler Pfad

Ist die Menge aller Lösungen der durch $\tau >0$ parametisierten Karush-Kuhn-Tucker Conditions:

$\mathcal{C}=\left\{\left(x_{\tau },{\lambda }_{\tau },s_{\tau }\right)\mid \tau >0\right\}$

Wenn die strikte Primal-dual zulässige Menge ungleich der leeren Menge ist, ist der Zentrale Pfad für $\tau$ eindeutig bestimmt.

Falls der Zentrale Pfad für ein $\tau \to 0$ gegen einen Punkt konvergiert, dann ist dieser Punkt eine Lösung für das Primal-duales pfadfolgendes Innere-Punkte-Verfahren.

Nachbarschaft