Graphen Theorie
Ein Graph ist vollständig, wenn alle Knoten mit allen anderen Knoten verbunden ist und er ist zusammenhängend, falls jeder Knoten von jedem anderen Knoten erreichbar ist.
Ein Graph ist bipartit oder vollständig bipartit, wenn man ihn in zwei Gruppen aufteilen kann, wobei es nur Kanten zwischen den Gruppen und nicht innerhalb der Gruppen gibt.
Bogen Teilgraph trennende Kantenmenge Schnitt
Strukturen
Kette → Pfad → Weg → Zyklus → Kreis Wald → Baum → Wurzelbaum → Binärbaum
Enthält jede Kante: Eulerpfad → Eulertour
Enthält jeden Knoten: Hamiltonweg → Hamiltonkreis
Ein Planarer Graph kann in zwei Dimensionen so verformt werden, dass es keine kreuzenden Kanten gibt. Mit einem solchen Graphen lässt sich dann auch ein dualer Graph bilden indem man jeder Fläche einen Knoten zuweist und diese an den Schnittstellen mit Kanten verbindet.
Kanten und Knotenmengen
Eine bedeckende Kantenmenge muss zu allen Knoten inzidieren. Dabei ist die Kantenbedeckungszahl die minimale Anzahl an Kanten, die man braucht um den Graphen zu bedecken. Die bedeckende Knotenmenge zusammen mit der Knotenbedeckungszahl funktionieren analog.
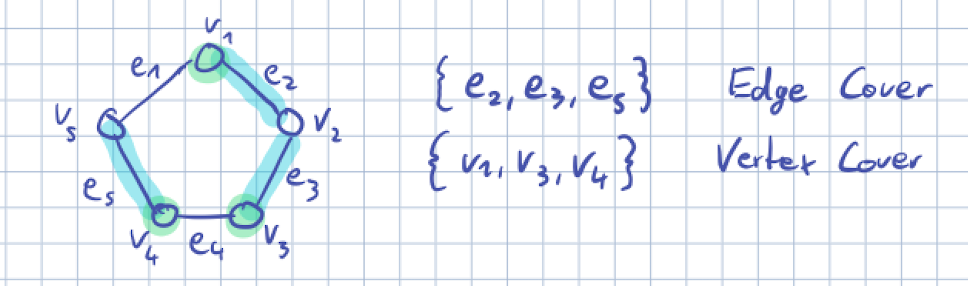
Der Satz von Gallai setzt bedeckende und unabhängige Knoten mit der Anzahl an Knoten in Verbindung.
Darstellung
Man kann einen Graphen in einer Matrix speichern. Da bei einer Matrix aber meistens viele Einträge Null sind nimmt man meistens eher eine Adjazenzliste zum speichern von Graphen.
Suchalgorithmen auf Graphen
Um Knoten in einem Graphen finden/suchen zu können kann man die beiden Algorithmen Breadth-first search und Depth-first search verwenden.
Sortierverfahren (auf Graphen)
Auspannende Bäume
Bei vielen Problemstellungen hilft es einen Minimalen Spannbaum auf einem Graphen zu finden.
Der Fundamentalschnitt und Fundamentalkreis sind wichtige Konzepte um einen Algorithmus zum Auffinden von minimalen Spannbäumen zu finden. Mit ihnen kann man die Schnitt-Optimalitätsbedingung und Pfad-Optimalitätsbedingung herleiten. Der MST-Algorithmus von Kruskal basiert auf der Schnitt-Optimalitätsbedingung und der MST-Algorithmus von Prim auf der Pfad-Optimalitätsbedingung.
Kürzeste Wege
Zum bestimmen kürzester Wege in einem Digraphen mit nicht negativen Kantengewichten kann man den Dijkstra Algorithmus verwenden.
Möchte man auch kürzeste Wege in einem Digraphen mit beliebigen Kantengewichten bestimmen muss man einen der folgenden Algorithmen verwenden.
Kürzeste Wege zwischen allen Knotenpaaren