Spatial Branch-and-Bound Verfahren

1. Untere Schranke

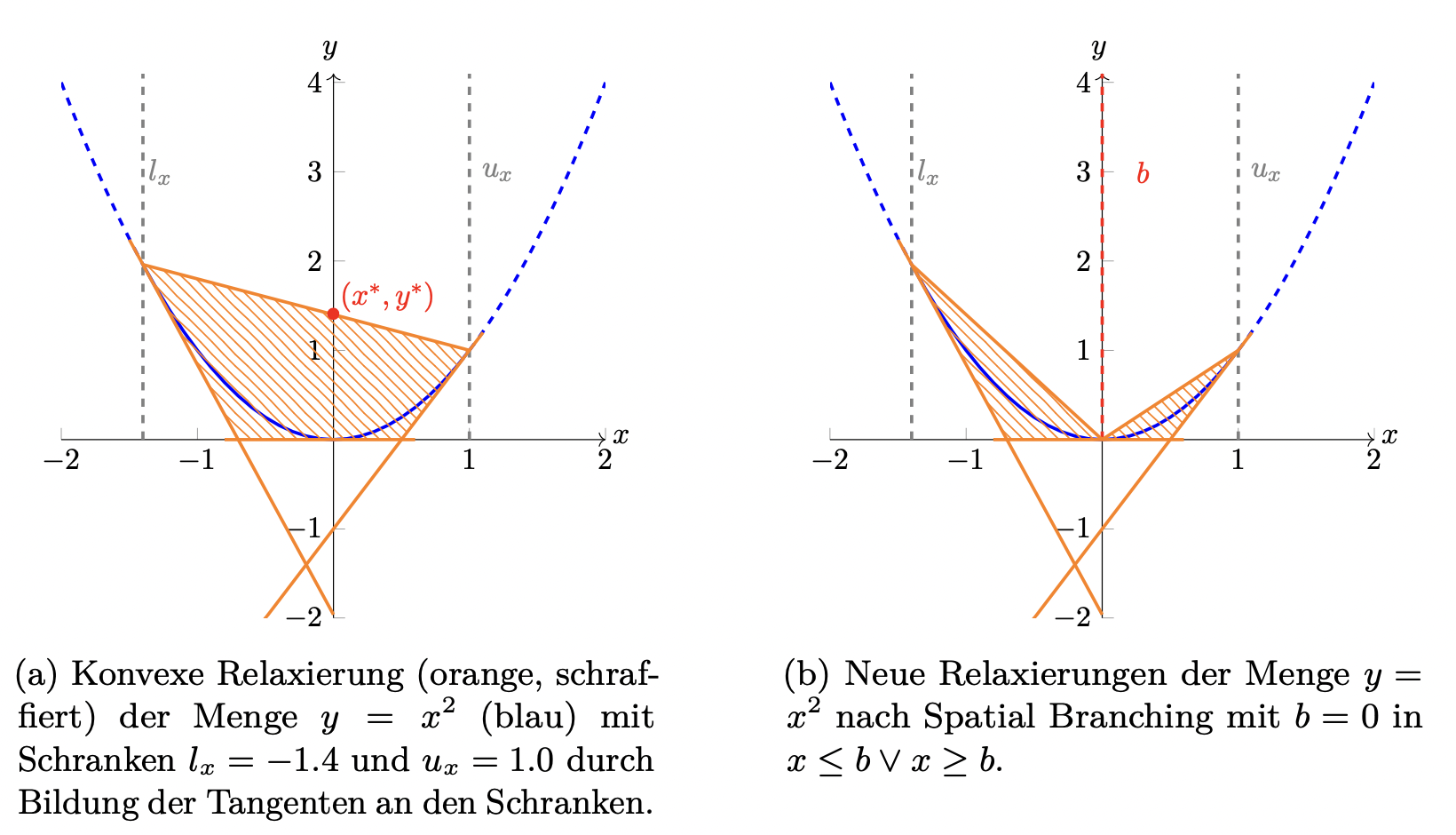
• Bestimme konvexe Relaxierung
• Lösung der Relaxierung liefert untere Schranke
  • Ist konvexe Relaxierung unzulässig so ist das Ursprungsproblem auch unzulässig
  • Wenn $\bar{u}-{\ell }_{\mathcal{R}}\le \epsilon$ für die kleinste obere Schranke $\bar{u}$ ist kann $\mathcal{R}$ keine $\epsilon$-optimale Lösung enthalten
  • Ist die Lösung zulässig so ist das Subproblem gelöst
  • Nächster Schritt

2. Obere Schranke

• Es wird keine zulässige Lösung gefunden
• Es gilt $u_{\mathcal{R}}>\bar{u}$
• Gilt $u_{\mathcal{R}}\le \bar{u}$, setze $\bar{u}=u_{\mathcal{R}}$ und lösche alle Subprobleme mit $\bar{u}-{\ell }_{\mathcal{R}}\le \epsilon$.
• Gilt $u_{\mathcal{R}}-l_{\mathcal{R}}\le ϵ$ dann ist das Subproblem optimal gelöst
• Nächster Schritt falls a oder b auftreten

3. Branching

• Ganzzahligkeit ist verletzt
  • wie beim Branch-and-Bound Verfahren vorgehen
• Mindestens eine möglicherweise nichtkonvexe Nebenbedingung ist verletzt
  • Wähle Variable, die Nebenbedingung $k$ am meisten verletzt
  • Teile Problem in zwei Subprobleme auf mit $x_i\le b$ und $x_i\ge b$
    Wähle $b$ nach Branching-Regel, zum Beispiel $b=x_i^{\ast }$

Algorithmus