Branch-and-Bound Verfahren

Das Branch-and-Bound Verfahren nutzt eine Relaxierung, die LP-Relaxierung, aus um ein MIP zu vereinfachen, indem es in Teilprobleme aufgespalten (Branch) wird.

Dabei verwendet es verschiedene Bedingungen (Bound) um nicht alle möglichen Teilprobleme lösen zu müssen:

• Prune by Infeasibility
• Prune by Integrality
• Prune by Bound

Ein Verfahren zum lösen von Gemischt-ganzzahligen linearen Optimierungsproblemen.

Für das Problem lässt sich der ZFW beschränken:

• $\hat{z}$ → Wert einer Optimallösung $\hat{x}$ von LP
• $z^{\ast }$ → Wert einer Optimallösung $x^{\ast }$ von MIP

Es gilt: $\hat{z}\le z^{\ast }$ denn mit der Relaxierung kann ein besserer ZFW durch eine für MIP unzulässige Lösung gefunden werden. Wenn aber $\hat{z}$ für MIP zulässig ist, dann ist es bereits die Optimallösung.

Das Problem lässt sich in Teilprobleme zerlegen:

• Sei $x$ gemischt-ganzzahlig
• Sei $s:={\hat{x}}_j\notin \mathbb{Z}$ mit $j\in \{1,...,p\}$

Dann ist

• $x$ zulässig für MIP mit $x_j\le \lfloor s\rfloor$ oder
• $x$ zulässig für MIP mit $x_j\ge \lceil s\rceil$

Seien

• $S$ zulässige Menge für MIP
• $P$ zulässige Menge für LP-Relaxierung

Zwei Annahmen müssen getroffen werden:

1. LP-Relaxierung besitzt keine zulässige Lösung oder eine Optimallösung, ist also nicht unbeschränkt.
2. Alle Koeffizienten in $A$ und $b$ sind rational (siehe Übung 7)

Vorgehen

Löse die LP-Relaxierung, dabei kann es zu folgenden Fällen kommen:

1. LP Relaxierung liefert eine ganzzahlige Lösung

Wenn die LP-Relaxierung eine ganzzahlige Lösung ergibt, so ist MIP gelöst.

2. LP Relaxierung liefert eine fraktionale Lösung

Wenn die LP-Relaxierung keine ganzzahlige Lösung ergibt, so ist die Lösung ein Wert $s$, der nicht ganzzahlig ist. Partitioniere $S$ mit $S_1:=S\cap \left\{x:x_j\le \lfloor s\rfloor \right\},S_2:=S\cap \left\{x:x_j\ge \lceil s\rceil \right\}$ Daraus entstehen zwei MIPs.

Stelle für die beiden MIPs die entsprechenden LP-Relaxierungen auf mit $P_1:=P\cap \left\{x:x_j\le \lfloor s\rfloor \right\},P_2:=P\cap \left\{x:x_j\ge \lceil s\rceil \right\}$ Beim lösen der LP-Relaxierungen können folgende Fälle auftreten:

1. Prune by Infeasibility
2. Prune by Integrality
3. Prune by Bound
4. Wenn das Problem einen kleineren ZFW als die beste obere Schranke (Prune by Integrality) hat, dann kann $S_i$ noch eine optimale Lösung enthalten. Es wird also erneut partitioniert mit $s_i:={\hat{x}}_j^i$ und den Mengen $S_{i1}$ und $S_{i2}$. Der Vorgang wird wiederholt.

Terminiertheit

Der Algorithmus stoppt, wenn alle Teilprobleme abgearbeitet sind. Das passiert in endlich vielen Schritten, wenn die ganzzahligen Variablen beschränkt sind. Die Anzahl an Teilproblemen kann aber exponentiell in der Anzahl der ganzzahligen Variablen wachsen.

Implementierung

Für eine effiziente Implementierung muss noch eine passende Node Selection Rule in Schritt 3 und Branching Rule in Schritt 13 des Algorithmus festgelegt werden.

Algorithmus

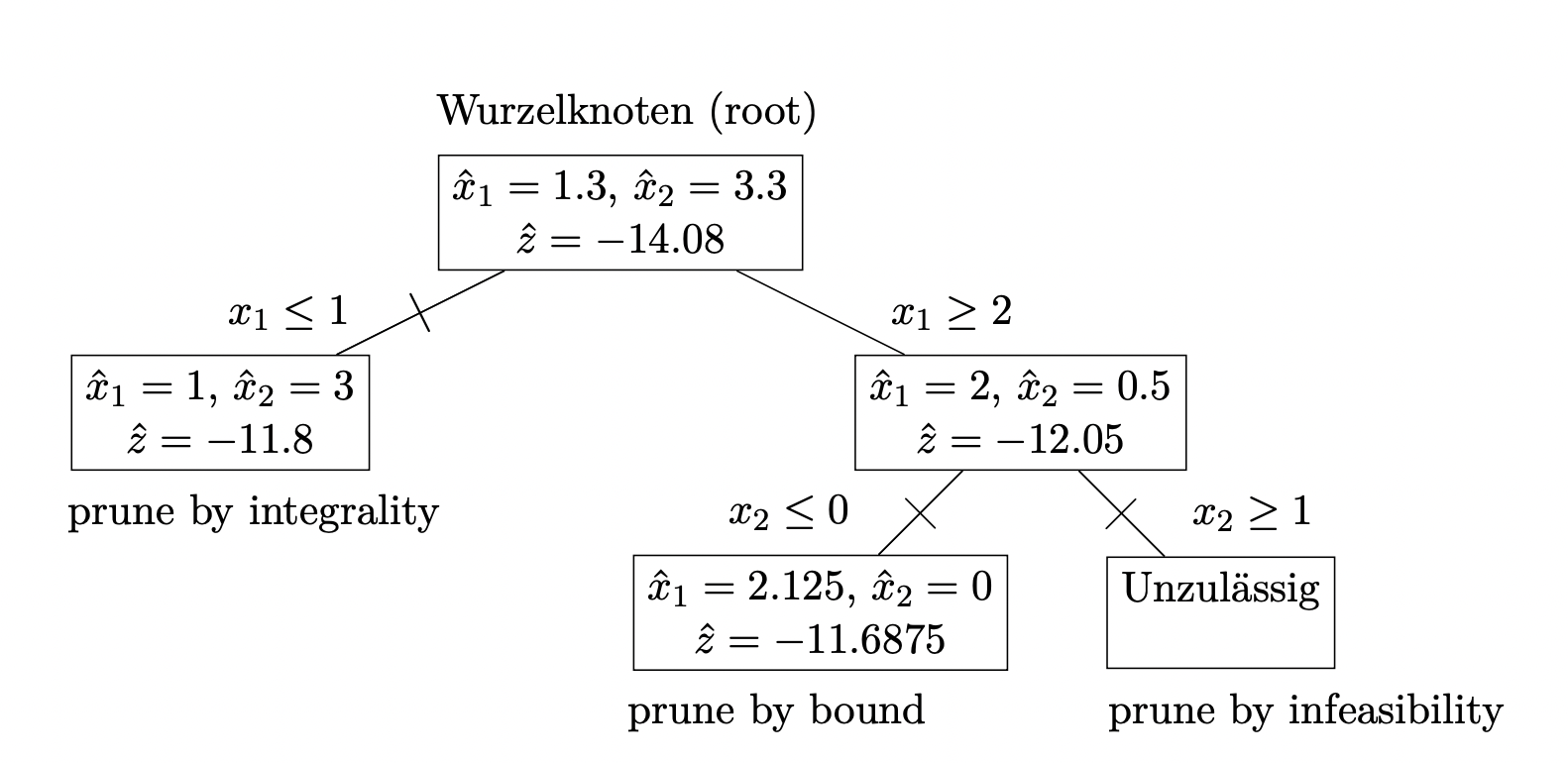
Beispiel

$\min \left\{-5.5x_1-2.1x_2:-x_1+x_2\le 2,8x_1+2x_2\le 17,x_1,x_2\ge 0,x_1,x_2\in \mathbb{Z}\right\}$

Oft wird ein Graph als Darstellung des Verfahrens verwendet: