Lagrange-duales Problem

${\sup }_{\lambda \in {\mathbb{R}}^m,\mu \in {\mathbb{R}}_{+}^{\ell }}{\inf }_{x\in {\mathbb{R}}^n}\mathcal{L}(x,\lambda ,\mu )$ Lagrange-Funktion, Lagrange-Multiplikatoren

mit dualer Zielfunktion:

$$d(\lambda ,\mu )=\underset{x\in {\mathbb{R}}^n}{\inf }\mathcal{L}(x,\lambda ,\mu )$$

Gradient der Lagrange-Funktion berechnen um $\mu$ und $\lambda$ zu bestimmen. Lösungen in die Zielfunktion substituieren. Daraus ergibt sich das Lagrange-duale Problem.

Beziehungsweise geschickt das Infimum bestimmen indem man Sachen, die nicht von $x$ abhängen rauszieht und das restliche Infimum überprüft.

→ siehe Übung 5

primale Zielfunktion: $p(x)={\sup }_{\lambda \in {\mathbb{R}}^m,\mu \in {\mathbb{R}}_{+}^{\ell }}\mathcal{L}(x,\lambda ,\mu )$

Beispiel

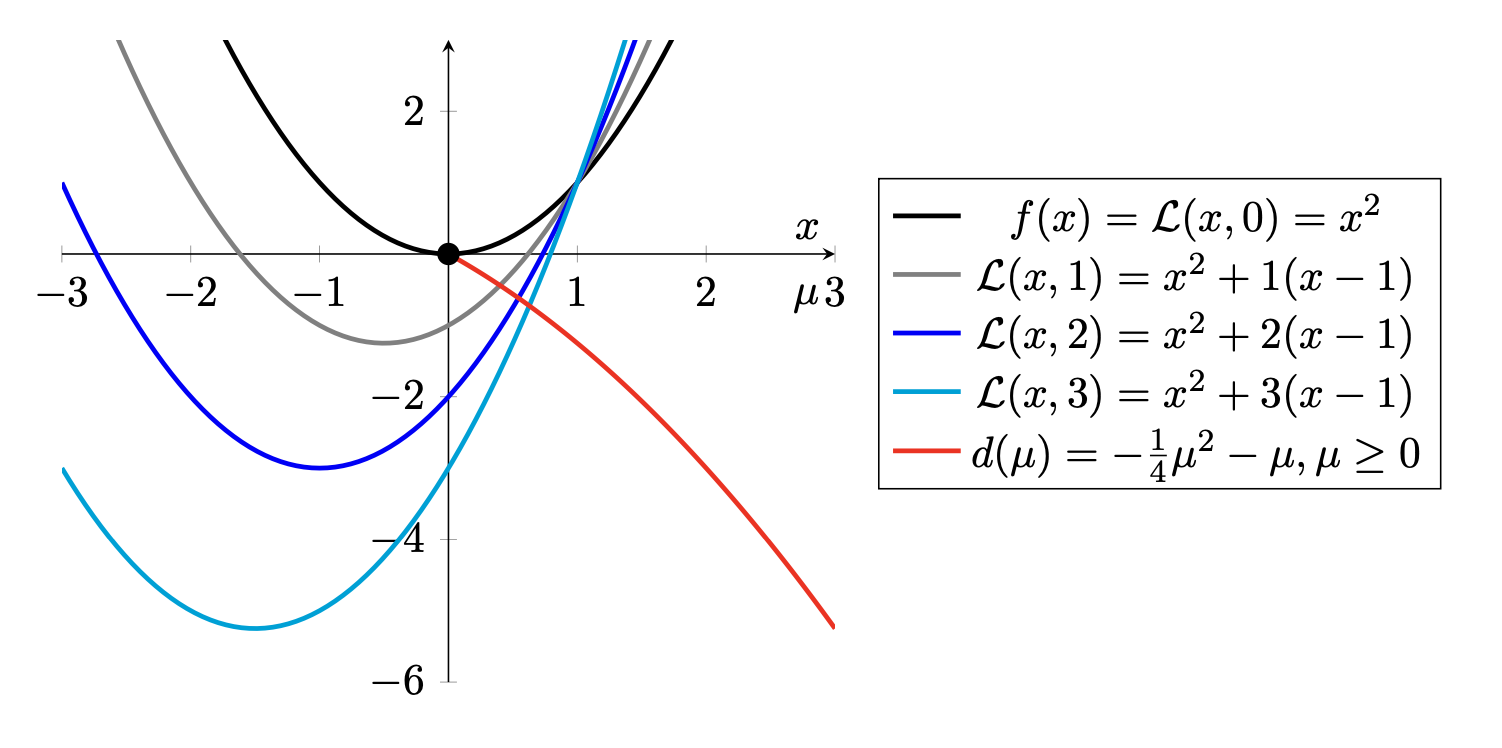
Wie man hier gut erkennen kann stellt das duale Problem stets eine untere Schranke des primalen Problems beziehungsweise der primalen Lösung dar.

In diesem Beispiel gilt sogar, dass der primale und duale Zielfunktionswert im Optimum gleich sind. Das ist allerdings nicht immer der Fall.

Other References

• Dual Constraint Relaxation
• Lagrangian and Dual Problem