Lagrange-Multiplikatoren
Zum Verständnis der Lagrange-Multiplikatoren:
Man kann an Punkten in der Nebenbedingung den Gradienten der Funktion und der Nebenbedingung berechnen. Man sieht, dass es sich um interessante Punkte handelt, wenn die Gradienten linear abhängig sind, also in die gleiche Richtung (evtl mit anderen Längen) zeigen. Die Gradienten sind dann kolinear, also ein jeweils Vielfaches des anderen.
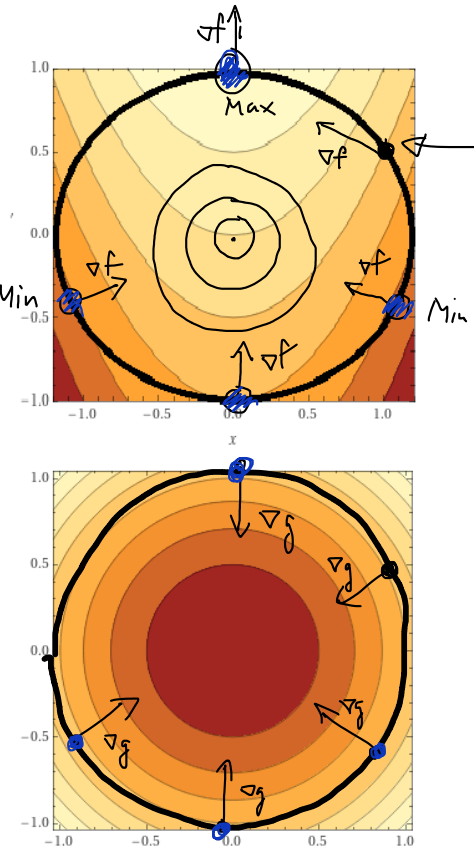
Aus dieser Beobachtung folgt dann die Idee des Lagrangefunktionals:
Um das Lagrangefunktional zu lösen berechnet man zunächst den Gradienten und sucht alle stationären Punkte. Man kann dann mithilfe der Hessematrix (wie in der Analytische Extremwertberechnung) entscheiden ob die Punkte Minima, Maxima oder Sattelpunkte sind. In manchen Fällen kann man das auch an der Nebenbedingung ablesen.
Lagrange mit mehreren Nebenbedingungen
Funktioniert genauso nur jz hat man n-Lambdas für alle n Nebenbedingungen. Man stellt genauso alle partiellen Ableitungen auf und versucht das Gleichungssystem zu lösen um die stationären Punkte zu finden.