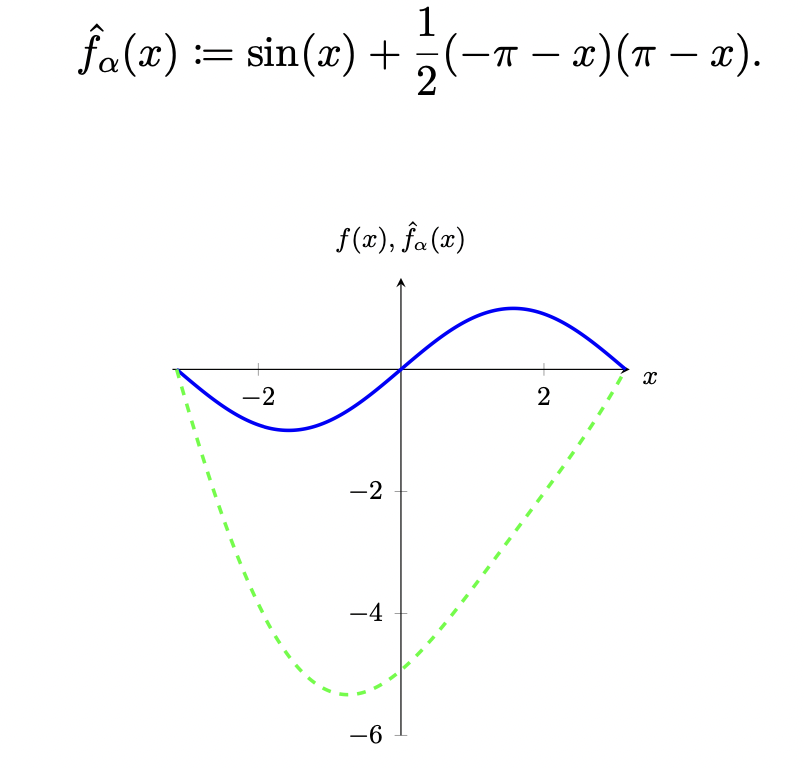
Alpha-Unterschätzer

Die zulässige Menge muss für den $\alpha$-Unterschätzer ein Quader mit unteren Schranken ${\underline{x}}_i$ und oberen Schranken ${\bar{x}}_i$ sein. Für ein $\alpha \in [0,\infty {)}^n$ heißt die Funktion ${\hat{f}}_{\alpha }(x):=f(x)+\underset{=:{\varphi }_{\alpha }(x)}{\underbrace{\sum _{i=1}^n{\alpha }_i\left({\underline{x}}_i-x_i\right)\left({\bar{x}}_i-x_i\right)}}$ Alpha-Unterschätzer von $f$.

Dabei ist ${\varphi }_{\alpha }$ der konvexe Teil der Funktion, da es ein Polynom zweiten Grades mit positiven Koeeffizienten ist. Das heißt, damit wir die Funktion konvex unterschätzen können sollte dieser Teil die Funktion überwiegen. Wir wollen $\alpha$ also groß genug wählen um Konvexität zu erreichen. Gleichzeitig sollte $\alpha$ aber auch so klein wie möglich sein um den enstandenen Fehler (Relaxierungsfaktor) so gering wie möglich zu halten. Eine gutes Maß für die Wahl von $\alpha$ bietet:

${\lambda }_{\min }+2{\min }_{i\in \{1,\dots ,n\}}{\alpha }_i\ge 0$ denn der Unterschätzer ist konvex falls diese Ungleichung gilt, wobei ${\lambda }_i$ dem kleinsten Eigenwert der Hessematrix von $f$ entspricht.

Es lässt sich der kleinste Eigenwert einer symmetrischen Matrix $A$ abschätzen durch: ${\lambda }_{\min }\Vert x{\Vert }^2\le x^{\top }Ax\le {\lambda }_{\max }\Vert x{\Vert }^2$ Beweis: Übungsaufgabe