Outer Approximation Verfahren
Häufig bessere Performance als das Branch-and-Bound Verfahren.
Die Idee ist statt NLP-Relaxierungen zu lösen MIP-Relaxierungen zu lösen, da wir MIPs verhältnismäßig gut lösen können.
Das Verfahren beruht unter folgenden
Annahmen
- ist Polytop
- Zielfunktion und nichtlineare Nebenbedinungen sind konvex und einmal stetig differenzierbar
- Eine Constraint Qualification ist bei jeder Lösung des NLP Subproblems erfüllt
Die größte Einschränkung ist die Konvexität, die gefordert wird. Der Algorithmus funktioniert auch auf nicht konvexen Problemen, dann ist allerdings nicht garantiert, dass er zu einem globalen Optimum führt.
Algorithmus
In diesem Verfahren werden abwechselnd NLP-Relaxierungen und MIP-Relaxierungen des Ursprungsproblem gelöst.
- Löse MIP
- Fixiere NLP-Relaxierung auf ganzzahligen Teil der MIP Lösung
- Löse NLP
→ 2 Fälle:
NLP hat Lösung
Für alle Lösungen des Ursprungsproblem gelten die folgenden Ungleichungen (siehe Lineare Approximation per Satz von Taylor) :
NLP ist unzulässig
Nach lösen des Zulässigkeitsproblem gelten diese Ungleichungen:
- Nun können die generierten Ungleichungen dem MIP hinzugefügt werden, welches erneut gelöst werden kann um neue Fixierungen zu berechnen.
- Der Algorithmus terminiert wenn das MIP nicht mehr zulässig ist

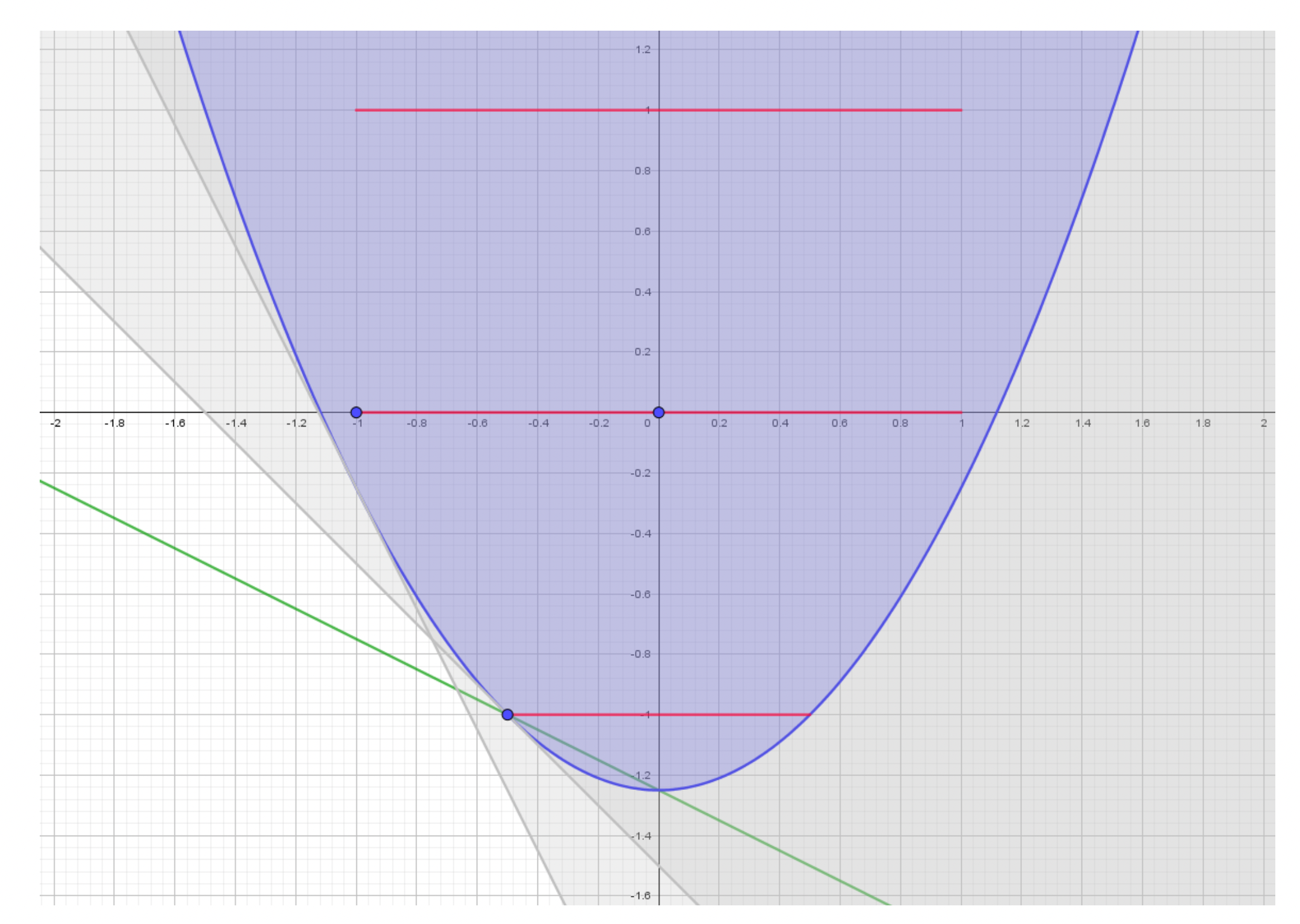
Arbeitsweise für ein Beispiel