Log-Likelihood

Because small values are very unstable in computers, we use the Log-Likelihood. It uses a sum and applies the logarithm to every datapoint.

$$\begin{array}{c}\mathbf{L}(\mathbf{\theta })=\prod _{i=1}^{N}p\left({\mathbf{s}}_i\mid \mathbf{\theta }\right)\stackrel{\ast }{=}\sum _{i=1}^N\log \left[p\left({\mathbf{s}}_i\mid \mathbf{\theta }\right)\right]=\mathbf{\ell }(\mathbf{\theta })\end{array}$$

Rewrite Log-Likelihood by inserting the Logistic Function and applying the logarithm to the sum

$$\begin{array}{rl}& \mathcal{L}(\theta )=\log \left(\prod _{i=1}^{m}P\left(y_i\mid x_i\right)\right)\\ & =\sum _{i=1}^m\log \left(g{\left({\theta }^{\top }{x}_i\right)}^{y_i}{\left(1-g\left({\theta }^{\top }{x}_i\right)\right)}^{1-x_i}\right)\end{array}$$

then again applying the logarithm to the exponents $={\sum }_{i=1}^m{y}_i\log \left(g\left({\theta }^{\top }{x}_i\right)\right)+\left(1-y_i\right)\log \left(1-g\left({\theta }^{\top }{x}_i\right)\right)$ then using the definition of the Logistic Function to get

$$\begin{array}{rl}& =\sum _{i=1}^m{y}_i\log \left(\frac{e^{{\theta }^{\top }{x}_i}}{1+e^{{\theta }^{\top }{x}_i}}\right)+\left(1-y_i\right)\log \left(\frac{1}{1+e^{{\theta }^{\top }{x}_i}}\right)\\ & =\sum _{i=1}^m{y}_i{\theta }^{\top }{x}_i+\log \frac{1}{1+e^{{\theta }^{\top }{x}_i}}\end{array}$$

and finally using the definition again to get $={\sum }_{i=1}^m{y}_i{\theta }^{\top }{x}_i+\log \left(1-g\left({\theta }^{\top }{x}_i\right)\right)$

We can use this much simpler form of the equation to calculate the Gradient of the Log-Likelihood:

$$\begin{array}{rl}& {\nabla }_{\theta }\mathcal{L}(\theta )={\nabla }_{\theta }\left(\sum _{i=1}^m{y}_i{\theta }^{\top }{x}_i+\log \left(1-g\left({\theta }^{\top }{x}_i\right)\right)\right)\\ & =\sum _{i=1}^m{y}_i{x}_{ij}+\frac{1}{1-g\left({\theta }^{\top }{x}_i\right)}(-g\left({\theta }^{\top }{x}_i\right)\left(1-g\left({\theta }^{\top }{x}_i\right)\right)x_{ij}\\ & =\sum _{i=1}^m{y}_i{x}_{ij}-g\left({\theta }^{\top }{x}_i\right)x_{ij}=\sum _{i=1}^m(y_i-g\left({\theta }^{\top }{x}_i\right)x_{ij}\end{array}$$

and the Hessian Matrix like this

$$\begin{array}{rl}& {\nabla }_{\theta }{\nabla }_{\theta }\mathcal{L}(\theta )={\nabla }_{\theta }\sum _{i=1}^m(y_i-g\left({\theta }^{\top }{x}_i\right)x_{ij}\\ & =\sum _{i=1}^m-g\left({\theta }^{\top }{x}_i\right)\left(1-g\left({\theta }^{\top }{x}_i\right)\right)x_i{x}_i^{\top }\end{array}$$

We can now use the Newton Method to iteratively calculate the best parameters: ${\theta }^{k+1}={\theta }^k-{\left(\frac{{\partial }^2}{\partial \theta \partial {\theta }^T}\mathcal{L}\left({\theta }^k\right)\right)}^{-1}\frac{\partial }{\partial \theta }\mathcal{L}\left({\theta }^k\right)$

For Gaussian

We then insert the Gaussian Distribution of $y$ like this:

$$\begin{array}{c}\begin{array}{rl}\sum _{i=1}^N\log \left[p\left({\mathbf{s}}_i\mid \mathbf{\theta }\right)\right]& =\sum _{i=1}^N\log \left[{\left(\frac{1}{2\pi {\sigma }^2}\right)}^{\frac{1}{2}}{e}^{-\frac{1}{2{\sigma }^2}{\left({\mathbf{y}}_i-{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i\right)}^2}\right]\\ & =-\frac{1}{2{\sigma }^2}\sum _{i=1}^N{\left({\mathbf{y}}_i-{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i\right)}^2-\frac{N}{2}\log \left(2\pi {\sigma }^2\right)\end{array}\end{array}$$

The Log-Likelihood can then be simplified to a negative constant times the Residual Sum of Squares (Also called the Loss) and adding another constant at the back.

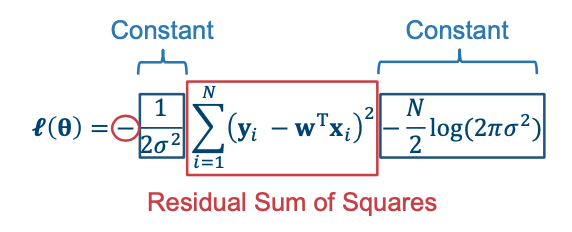
We now have a minus sign in the front. That is why we have to minimize the Residual Sum of Squares to maximize the Log-Likelihood.

The Loss is convex thus it has a unique minimum which can be calculated with:

• Gradient Descent
• Newtons Method
• Analytical solution