Correlation Analysis

Numerical data

→ Correlation, Covariance, Sample Covariance, Variance → Visual detection using Scatter Plot or Scatter Plot Matrices.

Nominal data

X = set of all distinct combinations of attributes Y = set of all tuples

Actual quantity: $c_{ij}=\#\left\{(a,b)\in Y\mid a=a_i,b=b_i\right\}=Y\left(\left(a_i,b_j\right)\right)$

Expected quantity in case of independence: $e_{ij}=\frac{{\sum }_{k=1}^m{c}_{ik}}{\#Y}\cdot \frac{{\sum }_{l=1}^n{c}_{lj}}{\#Y}\cdot \#Y=\frac{{\sum }_{k=1}^m{c}_{ik}\cdot {\sum }_{l=1}^n{c}_{lj}}{\#Y}$

${\sum }_{k=1}^m{e}_{ik}={\sum }_{k=1}^m{c}_{ik}\text{ and }{\sum }_{l=1}^n{e}_{lj}={\sum }_{l=1}^n{c}_{lj}$

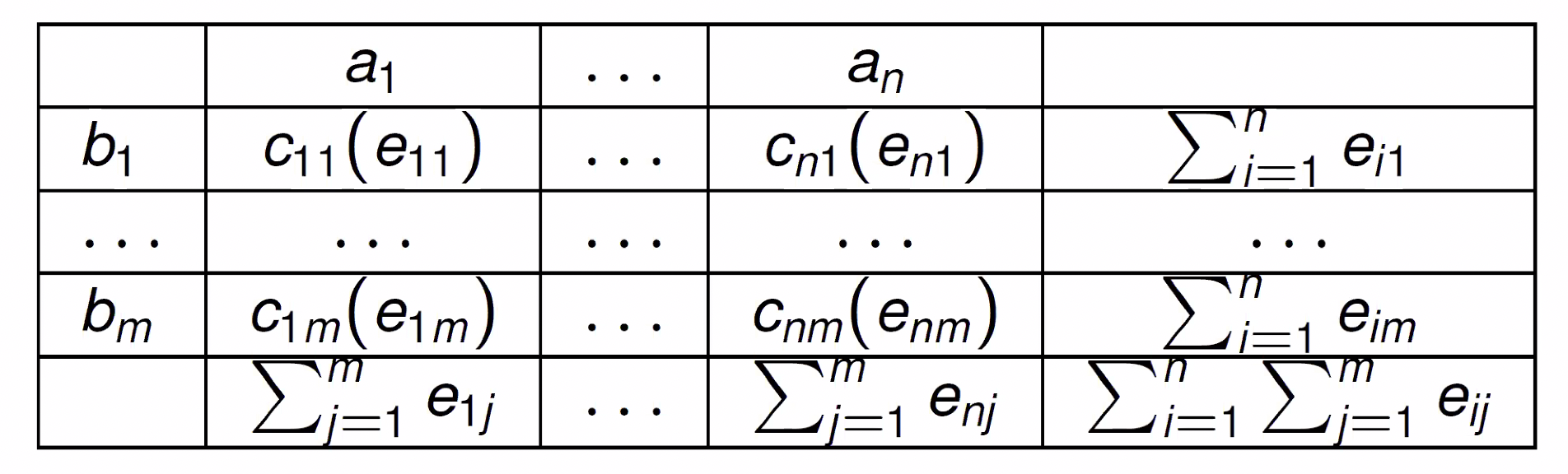
To determine Correlation you need to apply the Chi-Squared Test to the values in the table.

Python Implementation

def correlation(AS: pd.Series, BS: pd.Series):
    A = AS.unique()
    B = BS.unique()
    A = np.flip(A)
    B = np.flip(B)
 
    n = len(A)
    m = len(B)
 
    # Generate all possible combinations of values in A and B
    X = [(i, j) for i in A for j in B]
    Y = [(i, j) for i, j in zip(AS,BS)]
 
    nY = len(Y)
 
    def actual(i, j):
        count = 0
        for ab in Y:
            if ab[0] == i and ab[1] == j:
                count = count + 1
        return count
 
    def expected(i, j):
        s1 = sum([actual(i, k) for k in B])
        s2 = sum([actual(l, j) for l in A])
        return (s1 * s2) / nY
 
    # Calculate Expected and Actual matrices
    e_table = np.zeros((m,n))
    c_table = np.zeros((m,n))
    for i, b in enumerate(B):
        for j, a in enumerate(A):
            c = actual(a, b)
            e = expected(a, b)
            e_table[i, j] = e
            c_table[i, j] = c
 
    # Calculate Chi Squared Value
    chi = 0
    for i in range(n):
        for j in range(m):
            e = e_table[i, j]
            c = c_table[i, j]
            chi += (c - e)**2 / (e)
 
    return c_table, e_table, chi