Karush-Kuhn-Tucker Conditions

$$\begin{array}{rlrl}{h}_j(x)& =0& (j& =1,\dots ,m),\\ g_i(x)& \le 0& & (i=1,\dots ,\ell ),\\ \nabla f(x)+\sum _{j=1}^m{\lambda }_j\nabla h_j(x)+\sum _{i=1}^{\ell }{\mu }_i\nabla g_i(x)& =0,& & \\ {\mu }_i{g}_i(x)& =0& & (i=1,\dots ,\ell ),\\ {\mu }_i& \ge 0& & (i=1,\dots ,\ell )\end{array}$$

Die ersten beiden Bedingungen geben an, dass $x$ zulässig ist.

Die dritte Bedingung sagt aus, dass sich der Gradient von $f$ als Linearkombination der Gradienten der Nebenbedingungen $h_j$ und als konische Kombination (konische Hülle) der Nebenbedingungen $g_i$ schreiben lässt.

Hier ein Beispiel für die dritte Bedingung. Der negative Gradient liegt im Kegel (konische Hülle) der Nebenbedingungen, somit ist die dritte Bedingung mit bestimmten ${\mu }_i$ erfüllt.

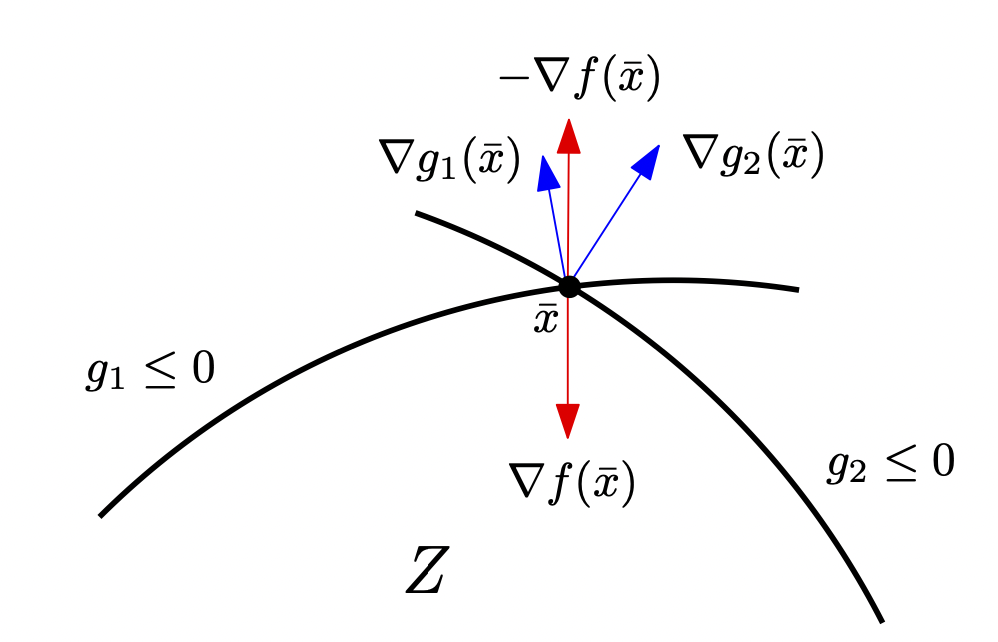
Die vierte Bedingung heißt Komplementaritätsbedingung.

$\lambda$ und $\mu$ sind Lagrange-Multiplikatoren.

Keine Restriktionen → Notwendige Optimalitätsbedingung erster Ordnung unrestringierter Probleme

Da die ${\lambda }_j$ kein Vorzeichen haben kann man für die Linearkombination auch schreiben: ${\sum }_{j=1}^m{\lambda }_j\nabla h_j(x)=-{\sum }_{j=1}^m{\lambda }_j\nabla h_j(x)$

Mit der Lagrange-Funktion lässt sich die dritte Bedinung auch als ${\nabla }_x\mathcal{L}(x,\lambda ,\mu )=0$ schreiben.

Wenn alle Funktionen zweimal stetig differenzierbar sind lässt sich die Hessematrix bestimmen als: ${\nabla }_{xx}^2\mathcal{L}(x,\lambda ,\mu )={\nabla }^{2}f(x)+{\sum }_{j=1}^m{\lambda }_j{\nabla }^2{h}_j(x)+{\sum }_{i=1}^l{\mu }_i{\nabla }^2{g}_i(x)$

KKT-Punkte bestimmen

• NLP in die Form bringen mit $f,g_i,h_i$.
• Gradienten aller Funktionen bestimmen
• Alle Fälle der Indexmenge der Aktiven Ungleichungsbedingungen durchgehen und auf Lagrange-Funktion testen
  • Jeweils auf die anderen Bedingungen wie $\mu >0$ testen
  • falls alle Bedingungen gelten → $x$ bestimmen
• Mit der Information, dass Ungleichung aktiv ist und dem $x$ kann $y$ berechnet werden
• Punkt auf Zulässigkeit testen (andere Bedingungen)
• LICQ überprüfen
• Für zwei aktive Ungleichungen können diese kombiniert werden um ein $x$ und $y$ zu berechnen. → Andere Bedinungen testen

ML4ENG

apply for the given problem:

$$\begin{array}{c}\begin{array}{c}{\alpha }_i\ge 0\\ y_i(w\cdot x-b)-1\le 0\\ {\alpha }_i\left[y_i(w\cdot x-b)-1\right]=0\end{array}\end{array}$$

Based on the last condition ${\alpha }_i=0$ or $y_i(w\cdot x-b)=1$ for each training point.

When ${\alpha }_i$ is not zero, we call the training point a support vector since it is right on the margin.

We can now use our previously derived function to calculate $w$ with our newly gained ${\alpha }_i$:

Depending on the sign of our result, the datapoint is either in class +1 or -1:

$$\begin{array}{c}y=\mathrm{sgn}(\mathbf{w}\cdot \mathbf{x}-b)=\mathrm{sgn}\left(\sum _{i=1}^n{\alpha }_i^{\ast }{y}_i{\mathbf{x}}_i\cdot \mathbf{x}\right)\end{array}$$