Faltung

Eine Faltung ist eine Operation auf zwei Zähldichten $f$ und $g$ mit ihren W-Maßen $P$ und $Q$ .

$$\begin{array}{rl}& f\ast g:\mathbb{Z}\to \mathbb{R}\\ & (f\ast g)(z):=\sum _{x\in \mathbb{Z}}f(x)g(z-x)\end{array}$$

Die Faltung ist auch eine Zähldichte auf $\mathbb{Z}$. Das Wahrscheinlichkeitsmaß zu der neuen Zähldichte ist $P\ast Q$.

Die Faltung ist assoziativ, kommutativ und distributiv. Damit kann man sie induktiv für mehr als zwei Zähldichten definieren.

Für den reellen Fall

$f_{x+y}(z)=\left(f_x+f_y\right)(z):={\int }_{-\infty }^{\infty }{f}_x(x)f_y(z-x)dx$ → Die sogenannte Lebesguie Dichte

Summe von Zufallsvariablen

Für zwei stochastisch unabhängige Zufallsvariablen mit ihren Verteilungen und Zähldichten gilt: $f_{X+Y}=f_X\ast f_Y$

Beweis

Den Beweis führt man über eine disjunkte Aufteilung:

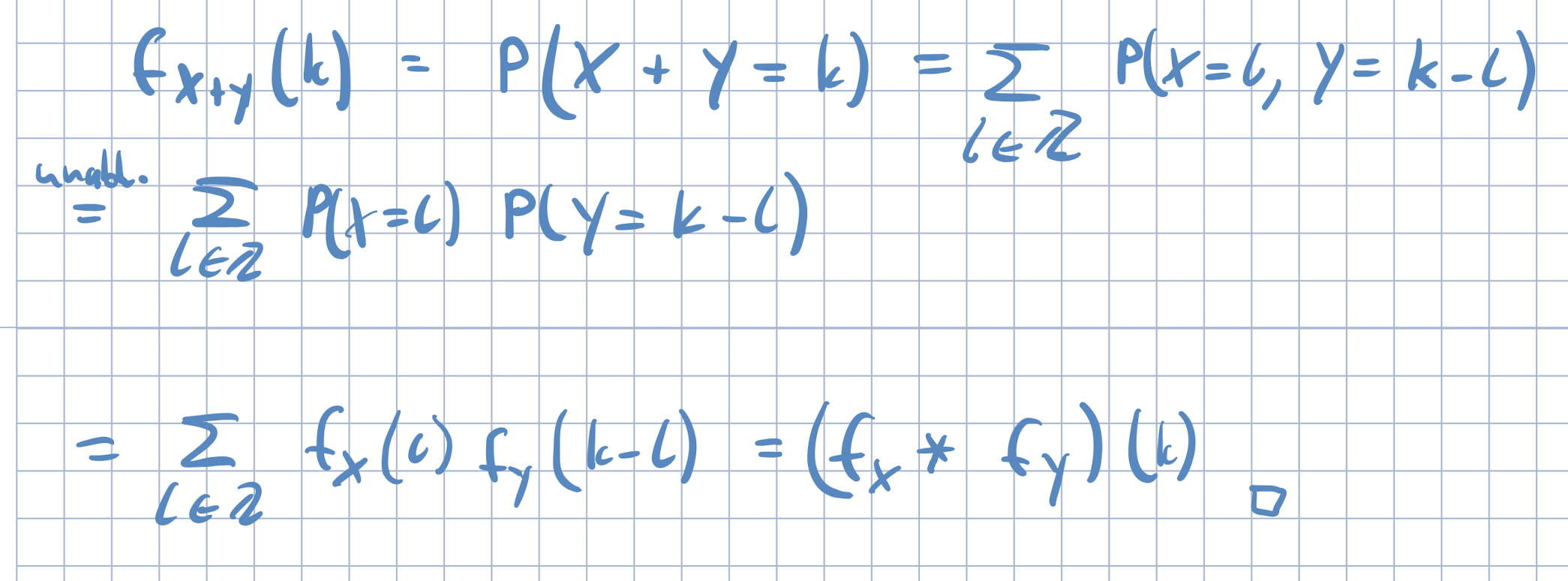
Resultate

Die Summe von $n$ normalverteilten Zufallsvariablen ist wieder eine normalverteile Zufallsvariable mit Erwartungswert gleich der Summer der Erwartungswerte und Varianz gleich der Summer der Varianzen.

Die Summe von Binomialverteilungen ist wieder eine Binomialverteilung mit $Bi{n}_{n+m,p}$. Außerdem ist die Summe von $n$ Bernoulli-Verteilungen eine Binomialverteilung.

→ Die Faltung tritt auch bei der Produktbildung von Potenzreihen und Polynomen auf → Erzeugende Funktion