Zufallsvariable

Motivation

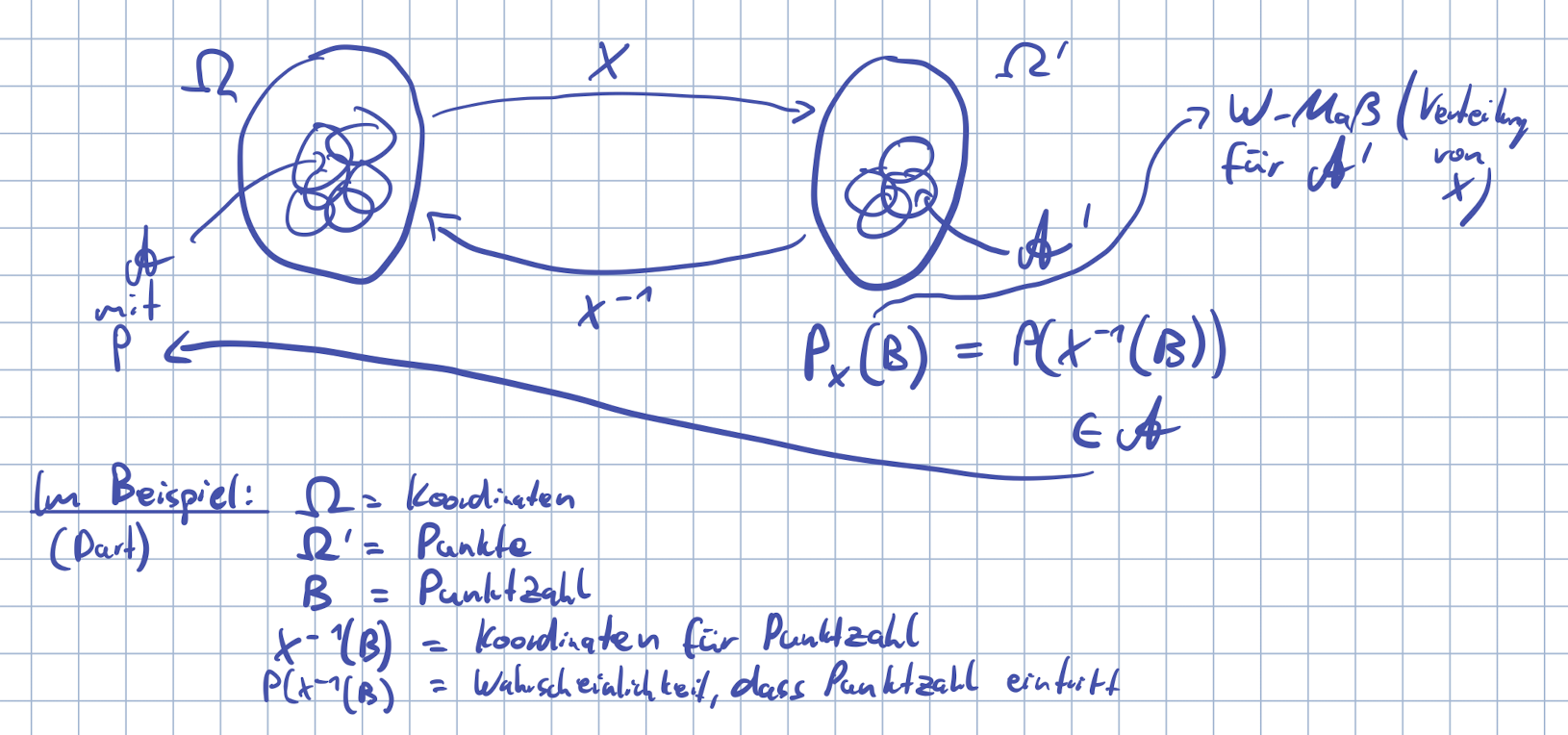
Manchmal ist man nicht unbedingt an einem bestimmten Ereignis interessiert sondern an einem Wert, der mit diesem Ereignis zusammenhängt. Zum Beispiel möchte man bei einem Dartwurf nicht wissen wie wahrscheinlich es ist eine bestimmte Koordinate zu treffen, sondern wie wahrscheinlich es ist in ein Feld (einer Menge an Koordinaten) zu treffen.

Definition

Eine solche Abbildung aus dem Wahrscheinlichkeitsraum in einen anderen Wahrscheinlichkeitsraum nennt man Zuffalsvariable. Dafür muss sie allerdings messbar bezüglich der beiden Sigma Algebren sein. Das heißt $X^{-1}(B)\in \mathcal{A}\text{fu¨r alle}B\in {\mathcal{A}}^{\prime }$

→ Eventuell ist es auch mal wichtig einen Messbarkeitsnachweis durchzuführen

Verteilung

Zu dieser Abbildung ist dann auch eine Verteilung $P_X$ definiert als $P_X(B)=P(X^{-1}(B))$

Stochastische Unabhängigkeit

Mehrere Zufallsvariablen sind stochastisch unabhängig, wenn für alle Ereignisse aus der Sigma Algebra gilt, dass die gemeinsame Verteilung der Zufallsvariablen das gleiche ist wie das Produkt der einzelnen Verteilungen

Abbildung

Beispiel

Ein Beispiel ist die Indikatorfunktion

Kurzschreibweisen

Mehrere Zufallsvariablen

gemeinsame Verteilung eindimensionale Randverteilung 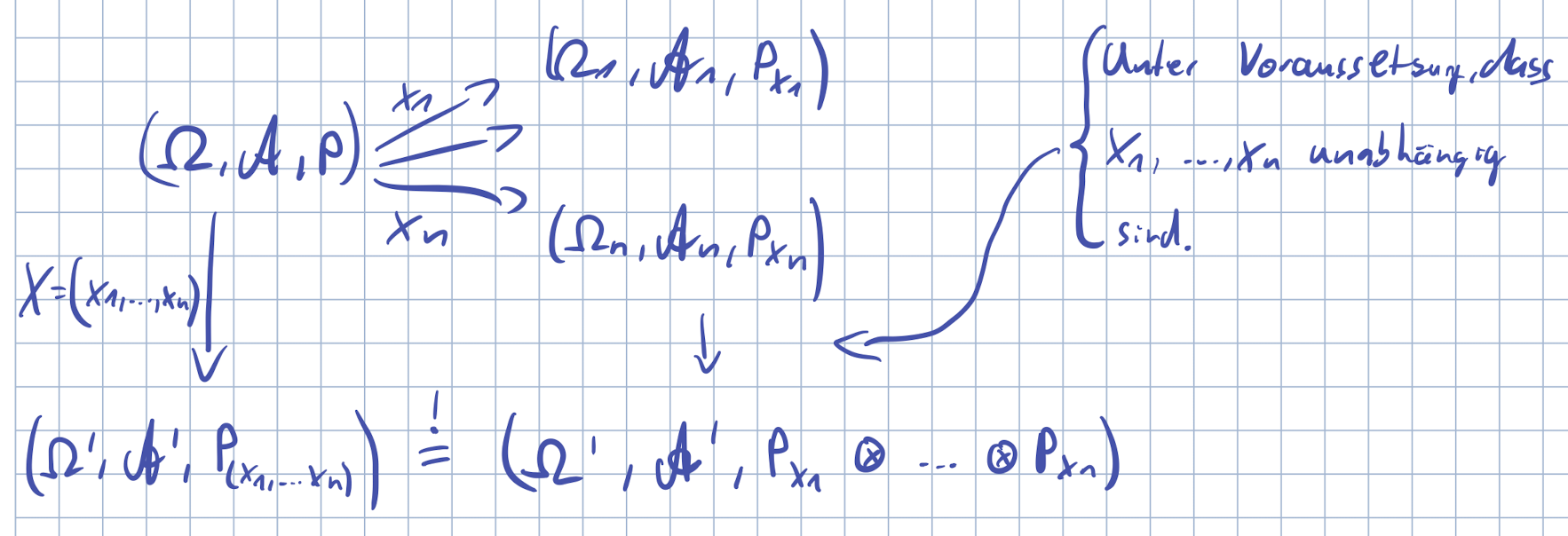Binomialverteilung